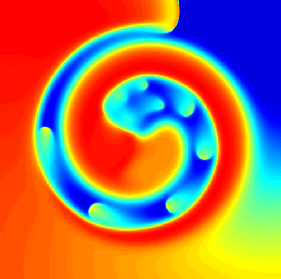
Using macros in the shaders: drawing the Julia set
The Julia set is very similar to the Mandelbrot set in its definition with a minor modification which produces much more reach features.
The sequence is constructed by the following sequence
\[ z_n = z_{n-1}^2 + c_0 \]
where \(z_0\), similar to the Mandelbrot set, is the coordinate of the point on the complex plane. \(c_0\) is a complex number that will be the same for all the points on the complex plane.
A point \(z_0\) is part of the set if and only if the above sequence remains bound.
We will analyze the complex points which their real and imaginary parts lie between -2 and 2 and assume \(c_0 = -0.9\).
We define the following macro to make the loop in the shader more understandable.
#define csqr(z) vec2((z).x*(z).x-(z).y*(z).y,2.*(z).x*(z).y)
Macros are pre-processed before compiling the shader code. This means whenever the compiler encounters csqr(z), it replaces it with vec2((z).x*(z).x-(z).y*(z).y,2.*(z).x*(z).y) and replacing z by whatever syntax that was passed to the macro. Since the preprocessing happens before compilation, and expressions are replaced verbatim as if they where typed, if you remove the brackets in expressions like (z).x and you pass something as a+b as z in the macro they will be replaced by a+b.x instead of (a+b).x which have completely different values. So, while macros provide performance improvements by avoiding branching, they should be used with care as they are significantly different from function definitions.
#version 300 es
precision highp float ;
precision highp int ;
out vec4 outcolor ; /* output of the shader
pixel color */
in vec2 cc ; /* input from vertex shader */
#define csqr(z) vec2((z).x*(z).x-(z).y*(z).y,2.*(z).x*(z).y)
// Main body of the shader
void main() {
vec2 z = cc*4. - vec2(2.,2.) ; /* Initial coordinate based
on pixel position */
vec2 c0 = vec2(-.9,0.) ; /* the constant c0 */
/* Iteration loop to march the iterative map for a 1000 times */
for(int i=0; i<1000; i++){
/* the Julia map */
z = csqr(z) + c0 ;
if (length(z)>2.){ /* if the point is not part of the set
color it black and end fragment shader */
outcolor=vec4(0.,0.,0.,1.) ;
return ;
}
}
/* if we managed to finish the loop the point is part of the set
so we can color it white */
outcolor = vec4(1.) ;
return ;
}
Notice how the macro csqr makes the code in the loop more understandable.
Running this program will produce the picture below.